laws of sine and cosine
2019-12-17 09:58I mentioned a couple years ago that I'd found proofs of them; I wasn't clear that proofs weren't part of my trig education along with sin(A+B), though lots of other identities were derived from addition and Pythagorean formulas.
The law of sine proof is easy and stayed with me. I don't recall my cosine proof (it was all in my head, no notes) and the one I came up with recently feels simpler (I recall grousing about grinding algebra) and different. Also like it would horrify the people who struggle with the concept of variables in algebra.
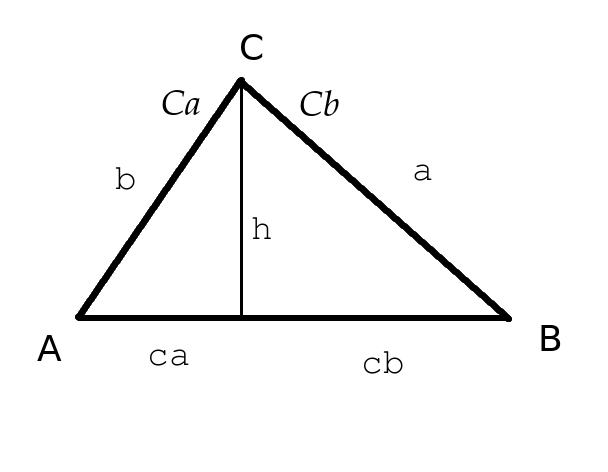
My drawing program sucked; Ca and Cb are supposed to refer to the two parts of angle C.
Law of Sines:
sin(A) = h/b
sin(B) = h/a
a*sin(B) = h = b*sin(A)
sin(A)/a = sin(B)/b
Voila.
Law of Cosines:
This has less obvious motivation, IMO; I like proofs that have a direction to them, rather than just happening to end up at your goal. But you take what you can get.
c^2 = (ca+cb)^2 = ca^2 + cb^2 + 2*ca*cb
ca^2 = b^2 - h^2, likewise cb^2 = a^2 - h^2
But also ca = b*sin(Ca) and cb = a*sin(Cb)
This is where the variable-strugglers would hate it, because we use *both* substitutions at once.
c^2 = b^2 - h^2 + a^2 - h^2 + 2*a*b*sin(Ca)*sin(Cb)
c^2 = a^2 + b^2 - 2*h^2 + 2*a*b*sin(Ca)*sin(Cb)
And let's do it again! h = b*cos(Ca) = a*cos(Cb)
h^2 = h*h and we'll use different substitutions for each h:
c^2 = a^2 + b^2 - 2*b*cos(Ca)*a*cos(Cb) + 2*a*b*sin(Ca)*sin(Cb)
Using cosine addition,
c^2 = a^2 + b^2 - 2*a*b*cos(Ca+Cb)
c^2 = a^2 + b^2 - 2*a*b*cos(C)
Voila!
Technically these proofs should be redone for obtuse angle triangles, to make sure they work when the perpendicular h is outside the triangle, but I haven't felt like being that rigorous.
The law of sine proof is easy and stayed with me. I don't recall my cosine proof (it was all in my head, no notes) and the one I came up with recently feels simpler (I recall grousing about grinding algebra) and different. Also like it would horrify the people who struggle with the concept of variables in algebra.

My drawing program sucked; Ca and Cb are supposed to refer to the two parts of angle C.
Law of Sines:
sin(A) = h/b
sin(B) = h/a
a*sin(B) = h = b*sin(A)
sin(A)/a = sin(B)/b
Voila.
Law of Cosines:
This has less obvious motivation, IMO; I like proofs that have a direction to them, rather than just happening to end up at your goal. But you take what you can get.
c^2 = (ca+cb)^2 = ca^2 + cb^2 + 2*ca*cb
ca^2 = b^2 - h^2, likewise cb^2 = a^2 - h^2
But also ca = b*sin(Ca) and cb = a*sin(Cb)
This is where the variable-strugglers would hate it, because we use *both* substitutions at once.
c^2 = b^2 - h^2 + a^2 - h^2 + 2*a*b*sin(Ca)*sin(Cb)
c^2 = a^2 + b^2 - 2*h^2 + 2*a*b*sin(Ca)*sin(Cb)
And let's do it again! h = b*cos(Ca) = a*cos(Cb)
h^2 = h*h and we'll use different substitutions for each h:
c^2 = a^2 + b^2 - 2*b*cos(Ca)*a*cos(Cb) + 2*a*b*sin(Ca)*sin(Cb)
Using cosine addition,
c^2 = a^2 + b^2 - 2*a*b*cos(Ca+Cb)
c^2 = a^2 + b^2 - 2*a*b*cos(C)
Voila!
Technically these proofs should be redone for obtuse angle triangles, to make sure they work when the perpendicular h is outside the triangle, but I haven't felt like being that rigorous.